Table of Contents

1 Overview

In this assignment you’ll draw 2D shapes by filling in individual pixels.

1.1 Logistics

You need to write every method you submit yourself. You cannot use other people’s code or find the method in an existing library. For example, you should not use Java’s Graphics class, PIL’s ImageDraw module, the CImg draw_* methods, the Bitmap Draw* methods, etc.

You are welcome to seek conceptual help from any source, but cite it in a comment if you get it from something other than a TA, the instructor, or class-assigned readings. You may only get coding help from the instructor or TAs.

Half of the points are for completing the required portions. You may add as many points as you wish on optional portions. Points in excess of 100% will carry over to other homework assignments.

1.2 Example files

All the example images in this writeup are hyperlinks to the input file that generated them. On some older browsers these hyperlinks might interact poorly with the mathematical formula rendering; if you have trouble accessing the files, please let the instructor know.

1.3 Structure and File Format

The same as HW0: your program will read a file from the command line and create a PNG file. The basic structure of the input file (lines with keywords and arguments, skipping unknown keywords, etc) remain unchanged.

2 Required

The required part is worth 50%

png

same as HW0

xyc, xyrgb

For this homework, when you see a vertex description line (xyc, xyrgb, or the optional xyrgba) you don’t draw it; you store it in an ordered list. Most other commands will refer to earlier vertices in a one-indexed way: 1 is the first vertex listed, −1 the most recent one listed. So, for example, in the following input file

png 20 30 hw1demo.png
xyc    2  3   #ff0000
xyrgb 10 29   0 127 0
xyrgb 19  9   0 0 255
trig 1 -1 2
xyc    0 29   #770099
trig 1 -2 -1

the first trig has vertices (in order) of (2, 3), (19, 9), and (10, 29); the second trig has (2, 3), (19, 9), and (0, 29).

Vertex indices will always refer to vertices earlier in the file. Vertex coordinates (x and y) may be decimal numbers. Colors will still be integers. You no longer need to support xy; all coordinates will have colors specified in this assignment.

linec i_1 i_2 hexcolorcode

Draw an 8-connected line of the given color using the DDA algorithm between the two vertices given. Ignore the colors of the vertices.

If the line extends farther in x than in y, DDA steps in x. At any given integer x, the line itself may have a non-integer y, but pixels have integer coordinates. Draw the pixel at the integer y of ⌊y + 0.5⌋.

The same logic applies to lines that extend farther in y than in x and their pixel’s x coordinates.

In the case where you start or end with an integer endpoint, include the smaller value but not the larger. For example, if stepping between 20 and 10, include 10 but not 20. This rule prevents adjacent lines with a shared endpoint from both drawing that endpoint; for example, if one line goes from 5 to 10 and another from 10 to 15, only the second will draw pixel 10.

trig i_1 i_2 i_3

Fill a triangle between the given vertices, linearly interpolating the vertex colors as you go. Use a DDA-based scanline algorithm: DDA step in y along the edges, then loop in x between these points.

Fill a vertex if its coordinates are inside the triangle, (e.g., pixel (3, 4) is inside (2.9, 4), (3.1, 4.1), (3.1, 3.9)) on the left (small x) edge of the triangle, or on a perfectly horizontal top (small y) edge. Do not fill it otherwise.

This coloring style is called Gouraud shading, hence the g in the keyword.

3 Optional

3.1 Colors

lineg i_1 i_2 (5%)

Linearly interpolates colors on lines

tric i_1 i_2 i_3 hexcolorcode (5%)

Fills a triangle as trig but uses the specified flat color, not linearly-iterpolated color

xyrgba or lineca/trica (10%)

Accept points xycrgba with a 4th color being an alpha (opacity) channel, and use that alpha in Gouraud shading (lineg and trig).

And/or, add lineca and trica that act like linec and tric but take an extra 2 hex digits in the color code, which are alpha (opacity). So #ff0000ff is opaque red, #0000ff07 is mostly transparent blue, etc.

Use the over operator discussed on Wikipedia: C_{o}={\frac {\alpha_{a}}{\alpha_{o}}}C_{a}+\left(1-{\frac {\alpha _{a}}{\alpha _{o}}}\right)C_{b}.

3.2 Shapes

polyec n i_1 i_2 … i_n hexcolorcode (10%)

Fill the given n-vertex polygon using the even-odd rule, as described in the SVG Spec.

Usually this is best done by going one scanline at a time, finding all of the edges that cross it, and then filling between pairs. Don’t forget to count vertexes that fall exactly on a scanline appropriately.

polynz n i_1 i_2 … i_n hexcolorcode (10%)

Fill the given n-vertex polygon using the non-zero rule, as described in the SVG Spec.

fann n i_1 i_2 … i_n (10%)

Goaraud fill a polygon between i_1 and each adjacent pair of subsequent vertices (e.g., i_1 i_2 i_3 and i_1 i_3 i_4 and …).

stripn n i_1 i_2 … i_n (10%)

Goaraud fill a polygon between each three consecutive indices (e.g., i_1 i_2 i_3 and i_2 i_3 i_4 and …).

linewc i_1 i_2 w hexcolorcode (10%)

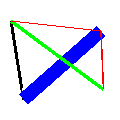
Draw a line as a rectangle with width w touching the two endpoints (line butt mode in the SVG spec).

3.3 Curves

cubicc i_1 i_2 i_3 i_4 hexcolorcode (15%)

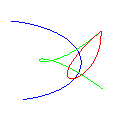
Draw a cubic bezier curve using the four control points given. I suggest using De Casteljau’s algorithm (or here) to break the curve into small lines.

beznc n i_1 i_2 … i_n hexcolorcode (10%)

Draw a bezier curve using the n control points given. I suggest using De Casteljau’s algorithm (or here) to break the curve into small lines.

cubicwc i_1 i_2 i_3 i_4 w hexcolorcode (5%)

Draw a cubic bezier curve of the given width. Usually this is done by turning the boundary of the curve into a polygon with a lot of vertices, adding two of the vertices at every step of De Caustlejau’s algorithm.

cubicg i_1 i_2 i_3 i_4 (10%)

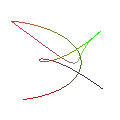
Draw a cubic bezier curve interpolating the vertex colors as you go.

cubicvwc i_1 i_2 i_3 i_4 w_1 w_2 w_3 w_4 hexcolorcode (10%)

Draw a cubic bezier curve where the width is interpolated along the curve. Usually this is done by turning the boundary of the curve into a polygon with a lot of vertices, adding two of the vertices at every step of De Caustlejau’s algorithm.

ucbnc n i_1 i_2 … i_n hexcolorcode (10%)

Draw a uniform cubic B-spline with the given control points.

A B-spline is just a tool for defining Bezier curves. The B-Spline control points p_1, p_2, p_3, p_4 define the cubic Bezier control points (p_1 + 4p_2 + p_3)\over 6, (2p_2 + p_3) \over 3, (p_2+2p_3) \over 3, (p_2 + 4p_3 + p_4) \over 6.

circle i_1 radius (15%)

Draw the outline of a circle centered at the given vertex with the given radius. Use the color of the vertex. You may assume the center vertex has integer coordinates and the radius is an integer.

3.4 Antialiasing

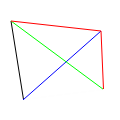
aalinec i_1 i_2 hexcolorcode (10%): Draw an anti-aliased line using the Wu algorithm. Use the over operator to compose transparent pixels.
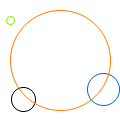
aacircle i_1 radius (10%): Draw an anti-aliased circle using the Wu algorithm. Use the over operator to compose transparent pixels.

3.5 Other

Feel free to add your own elements to the input set. Submit an input file named additional_.txt where _ is replaced by some number for each additional element you add. The input file should include a line beginning description that describes the new element. Points will be added at instructor discretion.