1 Overview
There are two options for this assignment.
- Option 1
- propose your own graphics task, agree with the prof how it will be graded, and than do it. If you go this route, it is probably best to speak with the prof in person, though email is also acceptable.
- Option 2
- An image manipulation assignment is listed below.
2 Loading filename.png in various languages
- C/C++
- Cimg or libpng (I’ve never used either to read
pngfiles in C or C++ so I don’t have details). - C#
- Use
System.Drawing.Bitmap:Bitmap img = Bitmap.fromFile("filename.png") - D
- Use imageformats:
auto img = read_image("filename.png") - Java
- Use
javax.imageio.ImageIO:BufferedImage img = ImageIO.read("filename.png") - Python
- Use pillow:
img = Image.open("filename.png")
The input examples use the following input files:
3 Advice
The structure of this assignment will be somewhat similar to those before: you’ll read an input .txt file and create an output .png file. The input .txt will generally begin with an instruction to read an RGBA .png file and generally end with an instruction to write an RGBA .png file of the same dimensions as the input.
You can probably make some progress working directly on the image files, but you will almost certainly find it easier to do the following:
- Use 0–1 color space
Convert all the 0–255 integers into 0–1 floating-point values as soon as you load an image.
Do not clamp pixel channel values to the 0–1 range during processing, but do do so before saving the image.
- Either use OO design or separate channels
You’ll want to be able to query and change R, G, B, H, S, L, V, and A channels on an image. There are two basic ways to do this:
- Separate channels
- Store R, G, B, and A as separate 2D arrays of floating-point values. Have functions that convert between color models (e.g.,
hue(r, g, b),red(h, s, l), etc.) - Channel-emulating accessors and mutators
- Store R, G, B, and A in an object, but provide functions like
getHueandsetSaturation.
- Clamp out-of-bound reads
- When you would read a color of a pixel outside of the image, use the color of the nearest pixel inside the image. Formally, this is a type of Neumann boundary condition.
- Use these channel definitions
V = \max(R,G,B)
\Delta = V - \min(R,G,B) (note: \Delta is not itself a channel, but is useful in computing several of the other channels).
S = \frac{\Delta}{V} (or 0 if V is 0)
There are other formulae for saturation. This version is typical for HSV color models; HSL often has a different form.
L = 0.299 R + 0.587 G + 0.114 B
There are many other formulae for lightness. This version is from ITU BT.601.
H = a piecewise-linear function:
- if \Delta = 0 then H = 0
- if V = R then H = \frac{G-B}{6 \Delta} (this might be < 0; if so, add 1 to it)
- if V = G then H = \frac{B-R}{6 \Delta} + \frac{1}{3}
- if V = B then H = \frac{R-G}{6 \Delta} + \frac{2}{3}
Recall that Hue is a circle, so 0 is closer to 0.9 than it is to 0.2.
For some optional parts you’ll need the reverse functions too.
To convert (H,S,V) \rightarrow (R,G,B)
- Let f(x) = \text{clamp}_{0,1}(2-|3-x|)
- R = V ((1-S)+S f((6H+3) \mod 6))
- G = V ((1-S)+S f((6H+1) \mod 6))
- B = V ((1-S)+S f((6H+5) \mod 6))
To change L
Given the way we’ve defined H, S, and L we cannot always change L without changing S (this follows from picking HSV’s version of S instead of HSLs). The following does the best we can do:
If old L is 0, use set all of R, G, and B to L.
Otherwise, try multiplying each of R, G, and B by (\frac{L_{new}}{L_{old}}), but only if all of the resulting values are ≤ 1.
Otherwise,
- Set V to 1; this will typically change L (among other values)
- Find the ratio t = \frac{1 - L_{new}}{1 - L_{changed}}
- Set R = 1 - (1-R)t and similarly for G and B.
See http://www.rapidtables.com/convert/color/ for another explanation (but note that their HSL uses different S and L than we have above).
4 Required Features
The required part is worth 50%
- input filename
- load the given RGBA png file as the current image.
- output filename
- save the current image as the given RGBA png file.
- monochrome channel
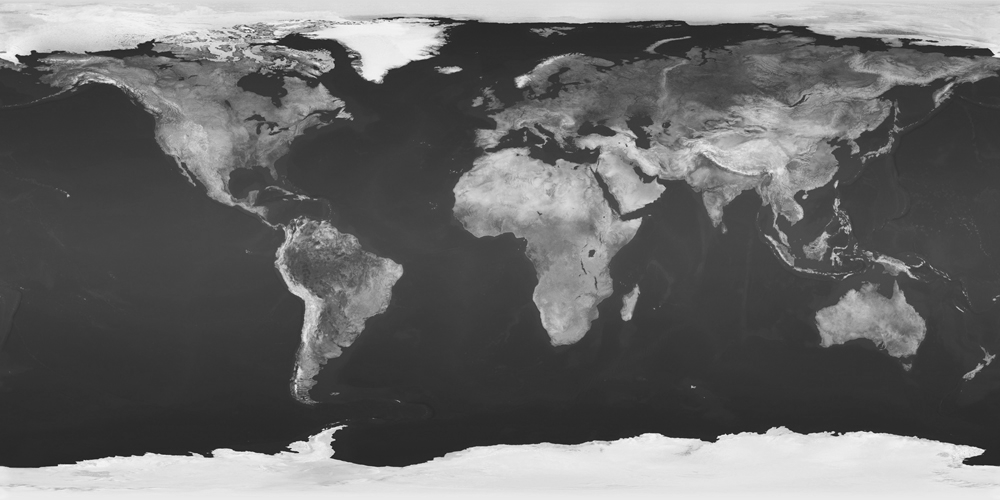
hw5monochromeL.txt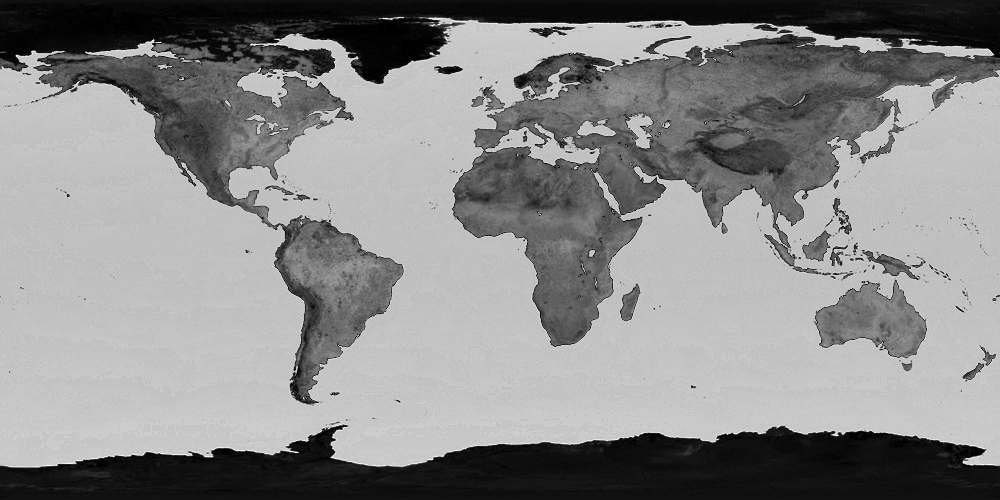
hw5monochromeS.txt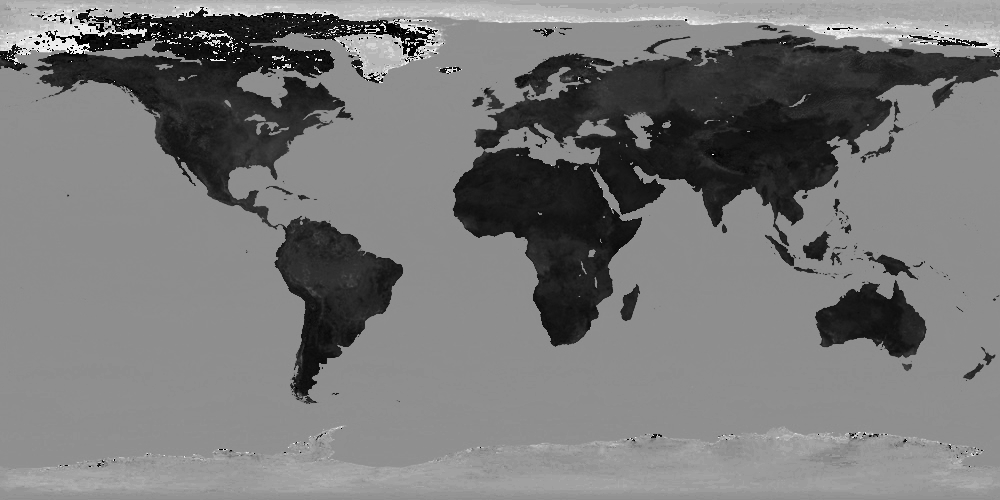
hw5monochromeH.txt Replace the red, green, and blue channels of the current image with a copy of the given channel. Set every alpha value to 1.You may assume that channel is one of the following eight strings:
red,green,blue,alpha,hue,saturation,value,lightness.This operator can typically be done in-place, though it also works if you copy the image.
- equalize channel

hw5equalize.txt Find the minimum and maximum value of the specified channel in the image. Then replace every pixels’ entry in that channel with channel\_value - minumum \over maximum - minimum.You may assume that channel is one of the following three strings:
red,green,blue.This operator can typically be done in-place, though it also works if you copy the image.
- gradient

hw5gradient.txt The Scharr 3-by-3 convolution filter \displaystyle \frac{1}{16}\begin{bmatrix}+3&+10&+3\\0&0&0\\-3&-10&-3\end{bmatrix} will find the y-gradient of the image; its rotated version \displaystyle \frac{1}{16}\begin{bmatrix}-3&0&+3\\-10&0&+10\\-3&0&+3\end{bmatrix} will find the x-gradient. You’ll need those gradients for many of the optional parts.For the required part, set the green channel of the image to the y-gradient of the lightness channel and both the blue and red channels to the x-gradient of the lightness channel.
This operator can typically cannot be done in-place; you’ll need to make a copy of the image first.
5 Optional Features
5.1 Pixel-based
- All Channels (20%)

hw5equalizeL.txt
hw5equalizeH.txt Extend all operations to work on any of the eight channels.When setting Hue, Saturation, or Value, assume that the other two of those are held constant. When setting Lightness, scale R, G, and B by new lightness ÷ old lightness.
Black is a special case for almost all of these; you are welcome to handle initially-black pixels however you wish.
- posterize channel n (10%)

hw5posterize.txt Clamp the given channel to just n distinct values, i \over n - 1 for i \in \{0, 1, 2, \dots, n-1\}. Move every pixel’s value in the given channel to the nearest of those values.You may assume that n \ge 2 and that channel is one of the following four strings:
red,green,blue,alpha.- dither channel n (10%; requires
posterize) 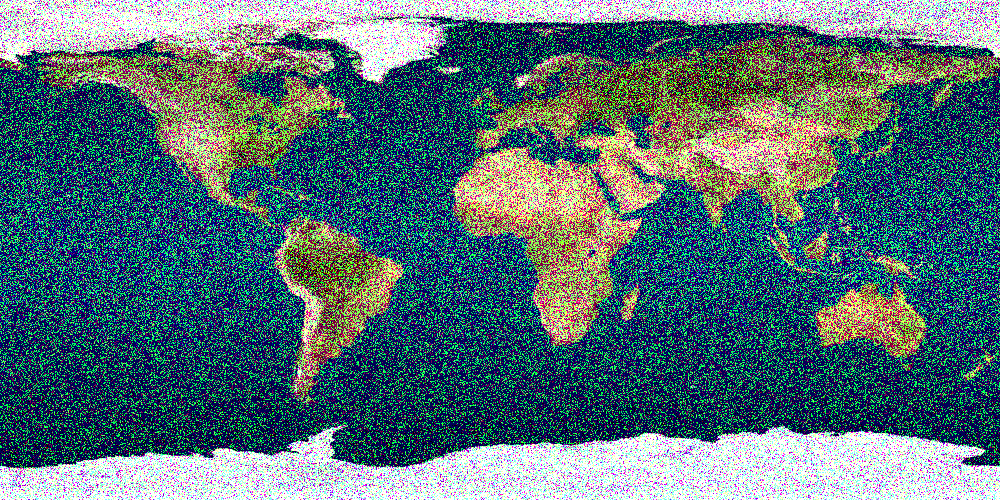
hw5dither.txt Clamp the given channel to just n distinct values, i \over n - 1 for i \in \{0, 1, 2, \dots, n-1\}. For any pixel whose value is between two of the output values, pick one of the two nearest values randomly with probability proportional to the nearness to each.You may make the same assumptions about N and channel as you did for
posterize.- rehue d_H (15%)

hw5rehue.txt Replace every color’s old hue H with H+d_H, wrapping back into the 0–1 range after the addition.
5.2 Convolution-based
- convolve channel w h n_1 n_2 … n_{wh} (20%)

hw5convolve.txt Apply the specified convolution filter to the given channel of the current image. You may assume that w and h are both odd numbers and that the channel is one ofred,green,blue, oralpha. The result of the convolution should become the new current image.- blur channel n (10%)

hw5blur.txt Convolve the given channel in x and in y by a discrete approximation of a Guassian filter with n entries. The entries should be normalized binomial coefficients (i.e., the nth row of Pascal’s triangle divided by 2^{n-1}); for example, n=7 will give the filter \frac{1}{64}\begin{bmatrix}1&6&15&20&15&6&1\end{bmatrix}.You may assume that n is a positive odd integer and that channel is one of the following four strings:
red,green,blue,alpha.- sharpen channel a (10%)

hw5sharpen.txt Sharpen the given channel of the image by convolving it with the matrix \begin{bmatrix}-0.1a&-0.15a&-0.1a\\-0.15a&1+a&-0.15a\\-0.1a&-0.15a&-0.1a\end{bmatrix}You may assume that channel is one of the following three strings:
red,green,blue.- edges min max (15%)

hw5edges.txt Compute the x and y gradients of the image in all R, G, and B and combine those six values using Euclidean distance (i.e., \sqrt{G_{r,x}^2 + G_{r,y}^2 + G_{g,x}^2+\dots}). Scale the resulting value so that min becomes 0 and max becomes 1. Use 1 - that result to set the R, G, and B values of the current image; set A to 1.
5.3 Non-local
- flood x y \Delta r g b a (10%)

hw5flood.txt Flood fill the image, starting with the pixel at coordinate x, y, with the color (r, g, b, a). Fill any pixel that is four-connected to another filled pixel and is within \Delta (which will be between 0 and 1) of the original pixel at coordinate x, y in all four of the RGBA channels.You may assume the initial color at (x,y) \ne (r,g,b,a)
- carve narrow and carve short (30%)
hw5carve.txt Use seam carving to make the image one pixelnarrower in width orshorter in height. Use gradient magnitude as a proxy for visual interest. In case of a tie (two or more seams of equally low total interest), pick one arbitrarily.To find the gradient magnitude, compute the x and y gradients of the image in all R, G, and B and combine those six values using Euclidean distance (i.e., \sqrt{G_{r,x}^2 + G_{r,y}^2 + G_{g,x}^2+\dots}).
- path x_1 y_1 x_2 y_2 r g b (30%)

hw5path.txt Use a shortest-path algorithm to connect the two input pixels (x_1, y_1) and (x_2, y_2). Fill the input pixels, and all pixels on the path between them, with the color (r, g, b, 1).Each pixel has eight neighbors. The
distance
to a neighbor is Euclidean distance (1 for 4-connect neighbors, \sqrt{2} for diagonal neighbors) times theflatness
of the neighbor being entered (there are various ways to compute that; we’ll use 1 \over \mathrm{gradient\;magnitude} + 0.1).To find the gradient magnitude, compute the x and y gradients of the image in all R, G, and B and combine those six values using Euclidean distance (i.e., \sqrt{G_{r,x}^2 + G_{r,y}^2 + G_{g,x}^2 + \dots}).
- advect chan d (20%)

hw5advect.txt Use back-advection to move colors around the image. The new color of pixel (x, y) should be computed as the color of the image at (x + g_x d, y + g_y d) where (g_x, g_y) is the gradient of the chan channel of the image at (x, y).When sampling a pixel at location (x,y) with non-integer coordinates, use a weighted average of the pixels at (\lfloor x\rfloor, \lfloor y\rfloor), (\lceil x\rceil, \lfloor y\rfloor), (\lfloor x\rfloor, \lceil y\rceil), and (\lceil x\rceil, \lceil y\rceil).