CS6160 - Theory of Computation Blog, UVa
Questions and answers regarding the CS6160 Theory of Computation class
material will be accumulated in this file throughout the semester.
Please browse through it often.
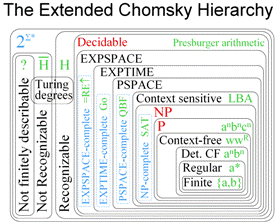 The questions in this file are organized by the following categories;
you may peruse this file sequentially, or jump directly to the
category of your choice by clicking on one of the following links:
The questions in this file are organized by the following categories;
you may peruse this file sequentially, or jump directly to the
category of your choice by clicking on one of the following links:
Q: What would a student need to do in order to receive the full 10% of
extra credit from additional readings and videos? Does it depend on
quantity read/viewed, or the quality of the responses from them?
A: It's basically the quantity of the EC submissions that counts the
most. You get the same extra-credit point for each paper / video
submission, no matter what opinion you offer on it. After all, its
your opinion, so nobody can second-guess you on your own opinion. To
get the full 10%, 36 EC submissions will suffice, as explained on the
course syllabus and in class (we deliberately leave the exact number
vague though, but the more, the merrier). Additional EC is possible
even beyond that, but no more than two submissions per day will be
credited (please see the strictly-enforced "no-binge"
submission policy on the
course
syllabus).
Q: You offered a bounty on building a Turing machine for extra credit.
Does it have to be physical, or could I build it in Minecraft?
A: Building a Turing machine in Minecraft is a wonderful idea! Please
feel free to do this for extra-credit.
Q: I have been working through the problem sets, and I was wondering
if you were planning on posting some solutions for the 2nd and 3rd
problem sets? I'm beginning to study for the midterm exam, and was
hoping I could make sure I understand the problem sets fully by seeing
some solutions.
A: I will post solutions to many of the problems of Set 1, but since
the midterm and final exam questions will come directly from the
(other) problem sets, I obviously can't post solutions to too many of
the other problem / sets, otherwise we will quickly run out of
problems to put on the exams. But keep in mind that some of the
problems were (or will be) solved in class, and many are also solved
in the weekly problem-solving sessions, so this (and also working in
groups of maximum size of six people) should cover you on most of the
solutions.
Q: Why is the class study group size limited to six people?
A: The group size is limited to avoid a surrealistic situation of say
people forming a "group" of say size 100, reaulting in them all
copying most of the solutions from each nother and each person ends up
doing very little learning. This would be an example of "crowd
sourcing", not a study group, and clearly defeats the spirit of
learning and self-improving, and this would also constitute
an honor code violation! If the group is of
reasonably small size (say six people at most), then it is very clear
to everyone in the group who is really honestly working on solving
problems, as opposed to just unfairly riding on the work of the
others. If a group has a good reason to want to add a seventh or
eight person, please come see us to explain the situation, and we may
allow it, but such cases should be rare.
Q: When exactly will the take home be available and when exactly will
it be due?
A: The midterm will take place shortly after mid-semester timeframe.
We will EMail the exact pickup / drop-off times when we get closer to
those dates.
Q: I am still slightly confused on how extra credit works as far as
extra credit readings. Is it just any overflow readings from the list
you gave us? Or things we find relevant out side of class also? For
example, the flux of the detection of gravitational waves I was doing
research on how they are able to compute Einstein's equations and
found this nifty article. Could I submit a response on something like
that for extra credit?
A: Basically we want to encourage everyone to read a lot and become
informed about a diversity of scientific and mathematical topics. So
anything that furthers that overarching goal is a wonderful thing in
our view. So yes, you can read other interesting articles in the same
vein as the ones that are posted on the class Web site, etc. And
indeed gravity waves are very cool (they were finally detected
experimentally recently after decades of trying, resulting in a Nobel
Prize).
In general, I want to encourage people to be proactive, curious,
knowledgeable, and informed - the rest is up to you (and I will do our
part to reward anyone whenever they take steps in that general
positive direction). I think that this is teaching and learning at
its best (and I wish my professors did more of this for me when I was
a student). I hope that my teaching philosophy and strategy makes
sense and is helpful to you.
Q: When we submit readings summaries/thoughts to the homework email,
should it be in the form of an attached document, or just plain text
typed into the email?
A: Either way is fine; we are working on implementing a Web-based form
that will make submissions even easier.
Q: Do we need to get "How to Solve It" for the class in addition to
the textbook?
A: All the red-font items on the
reading
list, including "How to Solve It", are required reading in this
course. There are live links there to the PDFs of all these items, so
"getting it" means you just need to click that link, and the PDF will
download to your PC. For example, "How to Solve It" is available for
download both here.
Please respect copyright laws however, and purchase copies of any
books that you are finding useful.
Q: I'm looking for some clarification on what should be included in
our write-ups. What types of things need to be there and what are some
other things we can add?
A: As stated on the
class Web site, please write up a summary of what you learned and
what you found interesting and/or surprising about each article /
video / app. Basically, convince the reader that you actually read /
watched it and that you payed attention while doing so. Of course, if
you choose to write more rather than less, that's fine.
Q: Just to clarify, although two assignments are due each week, if I
was to submit 6 the first week, would I would be fine for the next 3
mondays?
A: Yes, that would be fine - the idea is to not drop below the
2-per-week average overall, cumulatively speaking. This policy is
designed to help you avoid "cramming" at the end of the semester, and
also to help you retain more of the knowledge by pacing it more
evenly. Note that we will accept no more than two submissions per day
(so if you submit six readings the first week, these submissions will
presumably be turned in two per day across three days, etc.).
The best way to see the latest state-of-the-art in theory and
algorithms research is to look at the most recent papers published at
the top theory & algorithms conferences and journals, namely:
Most of the citations in the Web pages above do not include the full
text / PDF of the actual paper, but if you do a Google search for the
paper's title (and/or author list), you'll very quickly find the full
text / PDF of the actual paper (usually located off of the author's
home page).
To do specific topic searches for CS papers, two great online
bibliographic search resources are Citeseer and Google Scholar, which data-mine
the Web's publication archives and rank the papers by the number of
citations (i.e., how many other papers refer to a given paper), so the
most relevant papers tend to be listed first (like Google search
does). It also provides the PDF/PS to most of the papers there
(hundreds of thousands of CS papers in all). I highly recommended
both Citeseer and Google Scholar as
literature-searching resources!
Keep in mind that the sources listed above contain thousands of very
interesting papers (as well as hundreds of thousands of other papers),
so you can spend a lifetime on these sites and still not read
everything. So please don't get lost or discouraged by this mountain
of knowledge.
For a great introduction to computer science theory, I highly
recommend the Sipser
theory textbook (also available here).
For other theoretical topics, including algorithms, I also highly
recommend the Cormen
et al. algorithms textbook (especially the "advanced topics"
chapters on NP-completeness; also available here).
For a deeper understanding of a topic please track down the original
source papers mentioned in the "Chapter Notes" at the end of each
chapter, and also look at more recent papers published in the relevant
conferences and journals.
Enjoy! :)
Note: "extra credit" points will not hurt those who don't receive them
in this class, since at the semester's end, I take a first pass and
assign grades while *completely ignoring* extra credit points for
everyone; then, I take a second pass and raise (but never lower) the
grades of those who received enough extra credit points to bring them
up into a higher category w.r.t. the first pass.
This is really the only fair way to implement "extra credit" so it is
exactly that, namely "extra" (i.e., so it does not hurt those who
didn't earn it). Also, I have no grades "quotas" - if everyone aces
the course, then everyone will receive A's.
So, please view extra-credit as the positive and helpful opportunities
that they are intended to be.
Please feel free to ask our
TAs questions about any of the materials (my office hours are
right after each class meeting, or by appointment, or generally
whenever you can catch me in my office - please don't be hesitant to
find the TAs or myself whenever you need help).
Welcome to CS6160!
Please read the CS6160
Introduction and General Announcements.
Q: Should we submit an email for every single reading assignment or
problem that we solve, or can we submit one email that includes
several different items / solutions?
A: It is preferable to have a separate Email for each submission if
possible. This way, our accounting mechanism can better keep track of
all the different submissions, one per Email.
Q: Is there a deadline for turning in solutions to the problem sets?
A: There is no specific "due date" for the problem sets, and they
won't be formally collected & graded (i.e., they are not traditional
"homework" assignments). However, most of the midterm and final
questions will come directly from these problem sets, so the best
strategy is to solve as many of these problems as soon as possible,
work in study groups (of maximum size of six people), compare notes,
brainstorm often, etc.
Q: I just wanted to double check what you would like for us to turn in
for the assigned readings - do you want us to write a summary and
response to the article / video?
A: Yes - just EMail to homework.cs6160@gmail.com a paragraph or two
per article / video (and a page or two per book) describing what you
found interesting / surprising / cool about each.
Q: When is the time limit for when extra credit are still accepted?
A: Extra credit can be accepted all the way up to the end of the final
exam window. But three assigned readings are due each week (before
Mon at 11:59pm).
Q: I was wondering if you could clarify the honor code for this course
- what resources are we able to use to solve the problem sets? Are we
supposed to use just the powerpoints and our notes and the book, or is
outside research allowed? I ask because I know students have been
finding resources online to help supplement the material - for example
slides from other courses that are posted online from other schools.
Can you explain your expectation for us and policy?
A: For the problem sets, you can use all the outside resources you
want, including Web searches, working in groups with other people (of
maximum size of six), etc. The idea is that if you search a lot and
read a lot of materials, regardless of which sources they came from,
you'll still learn a lot in the process. Of course, it's still much
better training to try to work on / solve problems on your own
*before* looking up their solutions, etc. On the exam however, you
can only use your notes / book / slides, etc. but no outside help
(i.e., no Web searches, no collaborations, etc.)
Q: Are we allowed to use online resources to help us with extra credit
questions or do we have to come up with the answers without
assistance?
A: Its best if you work on the problems on your own first (or in a
group of maximum size of six people), and give them a good solid try.
There is still a lot of benefit in working on a problem, even if you
don't get the answer (just like exercising, but not necessarily
winning a competition trophy, is still good for you...). But looking
up answers without working on the problems first, is more like hiring
someone to exercise for you. :) After you worked on a problem for a
while and tried your best to solve it, it's OK to look up the answer
(say after a few days of thinking about it on and off).
On the definition of antisymmetric relations, lets use the slightly
modified definition, where a relation R is antisymmetric if R(a,b) is
not equal to R(b,a) unless a=b. This (i.e., excluding self-related
elements (a,a) from the antisymmetric constraint) allows a relation to
be reflexive and antisymmetric simultaneously. Thanks to the people
who pointed out this issue!
Q: Is every number imaginary?
A: Some "numbers" or *quantities* in general, are not
imaginary/complex, for example, a vector, or a matrix, or a quaternion, or an octonion. One question
is if you exponentiate i to the i, do you still get a complex number,
or does the resulting quantity *exits* the complex numbers, into say
the quaternions, or into some other, larger set. Just like when you
exponentiate the rational number 2 to the rational number 1/2, the
result sqrt(2) exits the rationals and falls into the set of reals
(that subsume the rationals).
Q: Question 13 asks "How many distinct boolean functions on N
variables are there?" Question 14 then generalizes this to N-ary
functions over two finite sets A and B. What does this question mean?
Q: Those questions basically ask how many *distinct* (i.e., different
/ not the same) functions are there of that particular type. So
considering *all* the different Boolean functions with N inputs (i.e.,
there are N inputs each being zero-or-one, and the function returns a
single zero-or-one output), how many such distinct functions are
there? (e.g., OR is one, and so is AND, and so is NOR, etc. all being
Boolean functions on two inputs). Questions 14 generalizes this
scenario to functions which are not necessarily Boolean any more
(e.g., the N inputs can each take on the values say {1,2,3,7,9} and
the function can return say one of the values {99, 111, 777}). BTW,
two functions are *distinct* iff they disagree (with their output) on
at least one input.
Q: RE "the rationals crossed with the integers", what is this set?
A: The rationals crossed with the integers is the set of all ordered
pairs such that in each of the ordered pairs in this set, the first
element is a rational number and the second element is an integer;
i.e., it is the set: { (a/b , c) | a, b, and c are all integers and b
in non-zero}
Q: Does the term dovetailing have any special meaning other than
interleaving? I have been used to using the later but not the
former. The Wiki explanation doesn't seem to suggest anything in
particular. Perhaps interleaving is just more general and may not
imply dovetailing as a procedure?
A: Dovetailing and interleaving are certainly similar concepts. The
description at http://en.wikipedia.org/wiki/Dovetailing_%28computer_science%29
seems too short and should probably cover more cases and examples.
There are more subtle examples of dovetailing / interleaving where we
take a systematic path through a very abstract mathematical space
(e.g., Chess / Go board positions, multivariate polynomials,
higher-dimensional matrices, hyper-graphs, etc.) where there may be no
nice and easy single "picture" to illustrate it graphically, like we
did in class with our "dovetailing" through the rational numbers. But
these are still (more general) instances of "dovetailing", or
"interleaving", however you prefer to think about it.
Q: For question #19, do you want a proof or just examples?
A: In #19, examples *are* proof, actually.
Q: If the complex numbers are closed under exponentiation, then when
you pick a complex number and apply an exponentiation operation, the
result is a complex number, right? When you were asking what was the
value of i^i, if that resulted in a non complex number, that would
imply that the complex numbers were not closed under the
exponentiation?
A: Yes - the question was general - namely to determine whether it is
always the case that (a+bi)^(c+di) is a complex number (as opposed to
something else), for any real a, b, c, d (except perhaps when they are
all zero, in which case the result 0^0 is undefined).
The case of i^i is a special case of the above general question (and
i^i happens to be equal to a periodic set of real numbers, as we
discussed in class yesterday). If i^i was not a complex number, then
the more general question above would be answered in the negative
through this counter-example. But since i^i is indeed a complex
number (and in fact even a real number), that does not settle the
general question above either way, and a more general proof is still
needed.
Q: In Problem Set 1, I am confused by the expression 2^{1,2} and how
to interpret it.
A: This is the "powerset" or set of all subsets, as described on page
5 of the handout I mentioned in recent Email (and which is also linked
from the class Web site) - see:
http://www.cs.virginia.edu/~robins/cs6160/basics.pdf
Q: In question 11b, what constitutes a function "mapping reals to
reals"? Does this mean any function that maps at least one real to
another real? Or does it only include functions whose domain is the
whole real line?
A: The domain and range of such functions is the set of real numbers
R, but note that such a function does not have to be a bijection, be
even defined everywhere on R. For example, the sqrt(x) function from
reals to reals is not defined on the negative reals, 1/x is not
defined at zero, and the function "f(x) = 1/(x-x)" is nowhere defined
on the reals, but these are all still "functions from reals to reals".
So the set of functions in this question refers to absolutely *all*
possible functions from R to R, regardless of their other properties.
Q: For Problem 20b which reads (L+ = L* - {^}), what does the "{^}"
notation mean? Is it correct to assume it's the circumflex character?
Also, does the subtraction notation mean "the language L* without {^}
in it?"
A: The symbol ^ in the context of formal languages denotes the empty
string (sometimes also denoted by the Greek letter epsilon). And yes,
the expression L* - {^} denotes set subtraction (i.e., the set L*
minus the set {^}).
Q: For True/False or Yes/No questions, how much explanation are you
looking for in the answers?
A: For any problem in this course (whether on the problem sets, exams,
or for extra credit), you should always supply an explanation/proof of
your answer. Basically, please explain your answers to me similarly
to how you would like me to explain my answers to you. It does not
have to be a *completely* detailed and formal writeup, but it must be
rigorous enough so that it contains all the essential insights, and
can be easily converted into a rigorous formal proof, if necessary
(i.e., please try to make your answers as convincing and detailed as
the explanations & proofs that I give in class).
Q: In 16 of Problem Set 1, is the question stating that you can only
have either 3 mutual strangers or 3 mutual acquaintances, but that you
can't have both? By 3 mutual acquaintances, does it mean that each
person in this group of 3 knows the other two people (ie A knows B, A
knows C, and B knows C)?
A: Mutual friends all know each other (i.e., each one knows each and
every one of the others). Similarly for mutual strangers. The
question asks for a proof that there always exists either a group of
three mutual strangers, or a group of three mutual friends, or
possibly both. (Or even larger groups of mutual friends or strangers;
but note that a group of four mutual friends also automatically
contains a group of three mutual friends - i.e., any subset containing
three of the four would constitute such a subgroup). So these various
case are not mutually exclusive.
Q: Question 11 on Problem Set 1 asks "What is the cardinality of each
of the following sets?" I am not sure what an answer "looks like",
since most of these sets are infinite.
A: The answer should indicate how "big" of an infinity each set is
(e.g., that of the Naturals, the Reals, the Powerset of the Reals,
etc.)
 EMail
to robins@cs.virginia.edu
EMail
to robins@cs.virginia.edu

 The questions in this file are organized by the following categories;
you may peruse this file sequentially, or jump directly to the
category of your choice by clicking on one of the following links:
The questions in this file are organized by the following categories;
you may peruse this file sequentially, or jump directly to the
category of your choice by clicking on one of the following links:
 EMail
to robins@cs.virginia.edu
EMail
to robins@cs.virginia.edu