Software Testing

Prime Path Coverage (PPC) Tutorial

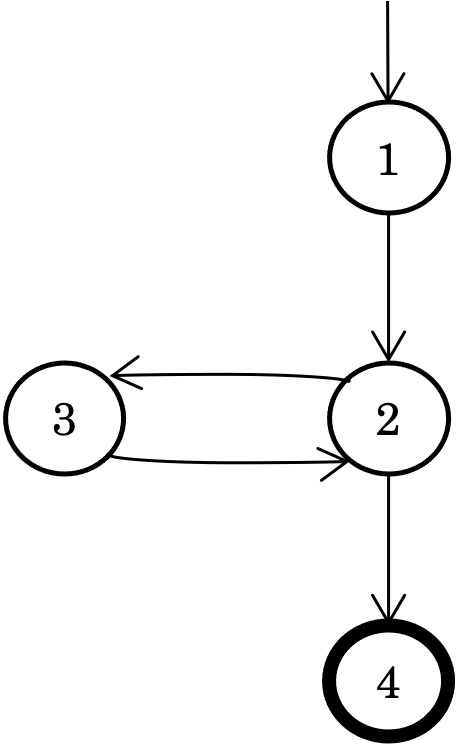
This brief tutorial demonstrates how to derive test requirements that satisfy Prime Path Coverage (PPC) criterion. We will use the graph above and then apply PPC to identify tests.

Definitions:

Prime path  = a simple path that is not a sub path of another path.
Simple path = a path without an internal loop (that is, no cycle inside the path)

Notations: 

!  represents a simple path that cannot be extended further. 
   The two possible reasons for this is that 
      - The path has reached a final node, or 
      - If the path is extended by one more node, it will create an internal loop, 
        which means it is no longer be a simple path.
          
*  represents a the simple path that is a loop (or cycle) 
   and thus cannot not be extended further 
      - If the path is extended by one more node, it will create an internal loop, 
        which means it is no longer be a simple path.

To derive a set of test requirements that satisfies PPC for the above graph

Start with individual nodes of the graph. List them as shown below. Note: L# denotes the length of a simple path.
```
L=0
[1]
[2]
[3]
[4]! 
```
Extend each of the paths without a symbol to another node via a valid edge and see if any of the simple paths need to be marked with an ! or *.
```
L=0          L=1
[1]          [1, 2]
[2]          [2, 3]
[3]          [2, 4]!
[4]!         [3, 2]     
```
Continue step 2 until all simple paths have a symbol next to them (i.e. they cannot be expanded further)
```
L=0          L=1             L=2
[1]          [1, 2]          [1, 2, 3]!
[2]          [2, 3]          [1, 2, 4]!
[3]          [2, 4]!         [2, 3, 2]*
[4]!         [3, 2]          [3, 2, 3]*
                             [3, 2, 4]!   
```
Note: [1, 2, 3] cannot be extended any further because the only edge that it can go is to node 2, creating the path [1, 2, 3, 2]. However, [1, 2, 3, 2] results in an "internal loop." Since a simple path cannot have an internal loop, [1, 2, 3] cannot be extended further.

Consider only the paths with symbols (! or *). Cross out all paths that are a sub path of another. A useful technique is to start from longest length and go to shortest length.

L=0          L=1             L=2
[1]          [1, 2]          [1, 2, 3]!
[2]          [2, 3]          [1, 2, 4]!
[3]          [2, 4]!         [2, 3, 2]*
[4]!         [3, 2]          [3, 2, 3]*
                             [3, 2, 4]!

The remaining paths with symbols are the prime paths that make up the test requirements needed to satisfy PPC for the given graph.
```
TR = { [1, 2, 3], [1, 2, 4], [2, 3, 2], [3, 2, 3], [3, 2, 4] }
```
If test paths are needed to be created, expand the given path as needed (expand left to start with an initial node; expand right to end with a final node).

Reminder: a test path must start with an initial node and end with a final node.

Multiple test requirements can be covered by one test path.

Example: [1, 2, 3] made in a test path is [1, 2, 3, 2, 4]. This test path would satisfy [1, 2, 3], [2, 3, 2], and [3, 2, 4].

Repeat this until all test requirements are covered by the set of test paths.

CC-BY-NC-SA 4.0 license.
Last updated 2024-02-27 11:54